Für Schüler biete ich zwei CDs an:
- Schülerversion: Sie enthält die wichtigen Teile der Vollausgabe. (Also ohne die vielen Texte für Lehrer/ Studenten)
- Vollversion: Die ganze Mathematik-CD mit allen Texten, und zusätzlich die große Sammlung an Abituraufgaben. Siehe https://www.mathe-cd.schule
Inhalt der Grundversion ⇒ DEMO zum Ansehen
Jeder Themenbereich
enthält eine große Zahl an Texten zu bestimmten Themen oder Fragestellungen. Das Menü hilft dabei, den geeigneten Text herauszufinden:
Die Texte enthalten den Lernstoff (Fakten, Methoden, Formeln), dazu Beispiele und
Übungsaufgaben zum Trainieren mit ausführlichen Lösungen).
Für die Oberstufe enthält die CD diese Themenbereiche:
1 Gerade und Kreis
2 Analysis-Grundlagen
-
- Zahlenfolgen, Reihen, Monotonie, Grenzwerte usw.
- Allgemeines: Stetigkeit, Differenzierbarkeit, Ableitungen aller Art, Monotonie, Extrem- und Wendepunkte. Symmetrie, Newton-Verfahren, L’Hospital, Methodentraining
- Ganzrationale Funktionen: Steckbriefaufgaben, Parabelaufgaben, Kurvenscharen
Trassierung, Alle Tangenten-Grundaufgaben - Gebrochen rationale Funktionen: Grundwissen, alle Methoden
- Wurzelfunktionen: Grundlagen, viele Trainingsaufgaben
- Exponentialfunktionen: Alle Grundlagen, viele Trainingsaufgaben, Wachstumsmodelle
- Logarithmusfunktionen: Alle Grundlagen, viele Trainingsaufgaben
- Trigonometrische Funktionen: Alle Grundlagen, viele Trainingsaufgaben
- Integration: Grundlagen, Flächenberechnung, Drehkörper, Bogenlänge
- Spezialthemen: Extremwertaufgaben, Regression, Ökonomie, Kostenfunktionen,
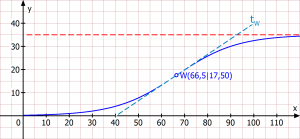
Stärkstes Baum-WACHSTUM am Wendepunkt
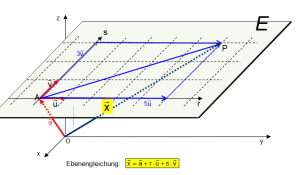
3 Vektorrechnung-Grundlagen
- Lineare Algebra: Linearkombinationen, Lineare Unabhängigkeit, Vektorraum
Lösung von Gleichungssystemen. - Vektorgeometrie: Alles über Geraden, Ebenen, Lagebeziehungen
Viele Spezialsammlungen zu besonderen Themen (Flugbewegungen, Gebäude,
Schattenprojektionen, Geometrische Körper) - Skalarprodukt und Vektorprodukt: Abstände und Winkel, Spiegelungen
- Kreis und Kugel: Vektorgleichungen, Tangenten und Tangentialebenen
4 Spezialthemen (vor allem für berufliche Gymnasien)
- Matrizenrechnung, Gauß-Verfahren für Gleichungssysteme
- Anwendungen: Übergangsmatrizen, Leontief-Modell, Markow-Ketten, Zustandsänderungen,
Spieletheorie, Bedarfsmatrizen, Kostenberechnungen - Lineare Optimierung: Simplexverfahren
5 Stochastik-Grundlagen
- Grundlagen: Statistische Erhebungen, Mehrstufige Ereignisse, Baumdiagramme, Vierfeldertafel, Urnenmodelle, Spezialaufgaben (dreimal mindestens, solange-bis)
- Bedingte Wahrscheinlichkeit
- Kombinatorik
- Verteilungen: Binomialverteilung, Hypergeometrische Verteilung, Erwartungswert,
Varianz, Standardabweichung, Normalverteilung - Signifikanztests
- Tschebyscheff
